C#에서 kd-tree 사용하기 (3차원, 2차원 상의 특정 점에서 가장 가까운 점 찾기)

문제의 정의

 3차원의 모델 데이터를 점들로 표현할 수 있다. 그리고 외부의 어떤 한 점이 있을 때, 이 점으로부터 가장 가까운 한 점을 모델 데이터에 속하는 점들에서 찾고자 한다. 

 

방법; kd-tree

 여러 가지 방법이 있을 수 있다. 가장 간단한 방법은 모든 점들을 저장하고 외부의 한 점과 거리를 모두 측정하여 가장 가까운 점을 찾으면 된다. 하지만 이 방법은 매우 오래 걸릴 수 있다. 이를 효율적으로 가장 가까운 점을 찾기 위해서 kd-tree를 사용할 수 있다.

 kd-tree는 수많은 점들을 효율적으로 접근할 수 있는 구조를 만들어 데이터들을 저장해두는 방식이다. 효율적으로 접근할 수 있는 구조로 되어 있기 때문에 원하는 점을 빨리 찾을 수 있다.

 데이터를 효율적으로 접근하기 위한 구조는 이진트리 구조(Binary Search Tree; BST)를 기반으로 한다. BST를 간략하게 설명해보자. BST는 여러 노드로 이루어져 있다. 이 중 하나의 노드는 값을 가지고 2개의 또 다른 노드들을 가지고 있다. 2개의 다른 노드는 똑같이 값을 가지며 또 다른 노드 2개를 가진다. 2개의 또 다른 노드를 자식 노드라고 하고 값을 가지는 노드를 부모 노드라고 명명할 수 있다. 예시를 위해 어떤 숫자의 집합이 있다고 가정하자. 이를 설명한 구조로 정리할 수 있다. 이를 그림으로 표현하면 다음과 같으며 마치 나무의 가지가 뻗어가는 모양이 나타난다. (트리 구조)

숫자의 집합을 이진 트리 구조로 나타난 예시

 

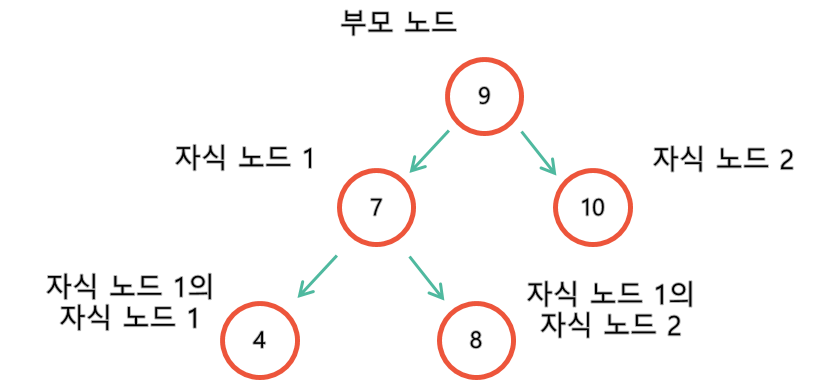
 이 구조를 자세히 보면 가장 가운데의 부모 노드에 여러 숫자들 중 가운데 숫자를 값에 넣었다. 이후 2개의 자식 노드에 각각 하나씩 작은 숫자, 큰 숫자를 넣었다. 이를 반복하여 정리된 구조라는 것을 알 수 있다.

 여기서 어떤 숫자와 가장 가까운 숫자를 찾는다고 생각해보자. 이러한 구조가 없다면 모든 값과 비교하며 가장 가까운 값을 찾으므로 많은 시간이 소요된다. 반면에 이진트리 구조를 사용한다면 하나씩 가지를 따라가며 빠르게 찾을 수 있다. 이를 그림으로 표현하면 아래와 같다.

숫자의 집합에서 어떤 값과 가장 가까운 값 찾는 두 방법의 비교

 

 kd-tree는 이러한 BST를 차원에 적용한 구조이다. 위에서 설명한 숫자의 집합으로 트리를 구성한다면 이는 1d-tree라고 볼 수 있다. x, y의 두 축의 값들을 가지는 점들로 트리를 구성한다면 2d-tree이다. x, y, z의 축을 가지는 3차원의 점들로 트리를 구성하면 3d-tree가 된다. 여기서 2d부터는 트리로 구조화되어 갈 때 각 축을 번갈아가며 노드들을 구성한다. 이를 쉽게 이해하기 위해 아래의 그림을 보자.

여러 차원에 따른 트리 구조화 설명

 

 그림에서 보이는 바와 같이 2d-tree의 경우 처음 부모 노드는 x축으로 정했다. 이후 다음 두 노드에 대해서는 y축으로 노드를 설정하였다. 이후 다음 4개의 노드(두 노드가 또 다른 자식 노트를 2개 가지므로)는 x축으로 정해진다. 3d-tree는 처음에는 x축, 그다음 층은 y축, 또 그다음 층은 z 축으로 정해져 있다. 그리고 다음 층마다 이를 반복하게 되어 있다.

 3차원의 모델 데이터를 3차원 점들의 집합으로 표현할 수 있다. 이를 kd-tree(3d-tree)에 구조화를 하여 저장한다. 이후 외부의 한 점에 대하여 가장 가까운 점을 구조화된 tree에서 각 축별로 비교해가며 찾으면 모든 점을 비교하는 것보다 매우 빠르게 찾을 수 있다.

 

C#에서 kd-tree 라이브러리 사용하기

 Visual studio로 C# 개발을 한다면 외부 라이브러리 패키지로 Nuget을 사용할 수 있다. kd-tree를 Nuget을 사용하여 설치하고 이를 사용해보자. 먼저 Nuget으로 kd-tree를 설치해보자. Visual studio 상단 메뉴 중 도구(T)-Nuget 패키지 관리자(N)-패키지 관리자 콘솔(O)를 선택하자.(이 글에서는 visual studio 2012를 사용하였음)

비주얼 스튜디오에서 Neget 패키지 관리자 콘솔을 실행

 

 하단에 나타난 패키지 관리자 콘솔의 PM> 부분에 Install-Package KdTree를 입력하여 실행하자. 

ㄹ

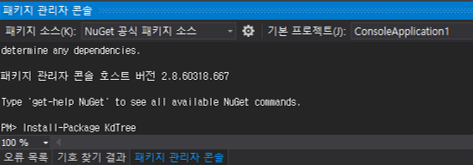
 몇 가지 문구와 함께 KdTree가 설치됨을 확인하자. 또 Solution-Project의 참조에 KdTreeLib가 추가되어 있음을 확인하자.

kd-tree 라이브러리를 Nuget으로 설치를 완료하였을 때 보이는 텍스트

 KdTreeLib가 참조에 추가된 모습

 

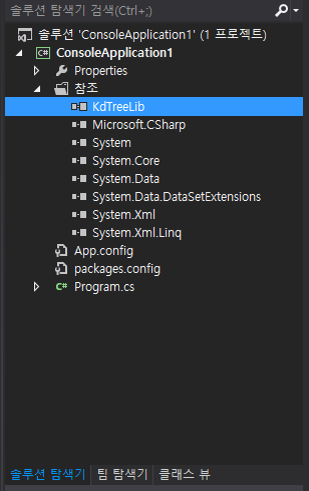
 Visual studio에서 콘솔 응용 프로그램을 만들어 테스트해보자. 먼저 kd-tree 라이브러리 사용을 위해 네임스페이스를 정의하자. 이후 kd-tree 라이브러리를 사용하여 트리 구조 변수를 생성하자. 이를 위해 아래와 같이 코드를 입력하자.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using KdTree;
using KdTree.Math;
 
namespace kdTreeTest
{
    class Program
    {
        static void Main(string[] args)
        {
            // define tree
            var tree = new KdTree<float, string>(3, new FloatMath());
        }
    }
}

 

 만들어진 트리 구조에 3차원 점을 임의로 만들어 넣어준다. 예제에서는 a, b, c라는 이름으로 3점을 추가하였다.

static void Main(string[] args)
{
    // define tree
    var tree = new KdTree<float, string>(3, new FloatMath());
 
    // define each points (3 points)
    // {x, y, z}, point name
    tree.Add(new[] { 50.0f, 80.0f, 80.0f }, "a");
    tree.Add(new[] { 20.0f, 10.0f, 20.0f }, "b");
    tree.Add(new[] { 20.0f, 10.0f, 10.0f }, "c");
}

Reference

• nugetmusthaves.com/Package/KdTree
• github.com/codeandcats/KdTree
• accord-framework.net/docs/html/T_Accord_Collections_KDTree_1.htm
• jackpot53.tistory.com/17
• makefortune2.tistory.com/52
• adioshun.gitbooks.io/3d_people_detection/content/ebook/part02/part02-chapter02.html
• makemethink.tistory.com/134

[자료구조] 9-3. 이진 탐색 트리의 연산 (2)

Octree-kdTree · 3D_People_Detection

26. BST (Binary Search Tree, 이진탐색트리) 알고리즘

균형 이진탐색트리(Balanced Binary Search Tree)

KDTree(T) Class

codeandcats/KdTree

KdTree